HiFi Multifluid Modeling Framework

HiFi is a user-friendly massively parallel adaptive high order finite element (a.k.a. spectral element) modeling framework designed for multi-fluid numerical simulations in two- and three-dimensional geometries (Glasser & Tang 2004; Lukin 2008). The manuscript Overview of HiFi - implicit spectral element code framework for multi-fluid plasma applications by Lukin et al. (2016) describes the overall algorithmic structure and the main features, as well as provides several application examples, of the HiFi framework.

The framework has been developed by the HiFi team with Dr. Vyacheslav Lukin and Dr. Alan Glasser as the primary developers.

A key feature of HiFi is the very general 'flux-source' form of the system of partial differential equations (PDEs). The combination of a user-friendly interface structure with minimal overhead and robust numerical methods designed to allow the code to utilize high performance computing platforms is the hallmark of the HiFi framework. The high-order spectral element representation enables HiFi to take advantage of the exponentially convergent spatial discretization, while the discretization operator remains localized and therefore amenable to parallelization. A grid adaptation algorithm enables the code to re-map the grid, as necessary, whenever fine scale structures dynamically arise and begin to require higher resolution anywhere within the domain.

The code has undergone rigorous verification testing (Lukin 2008; Meier et al. 2010; Lowrie et al. 2011).

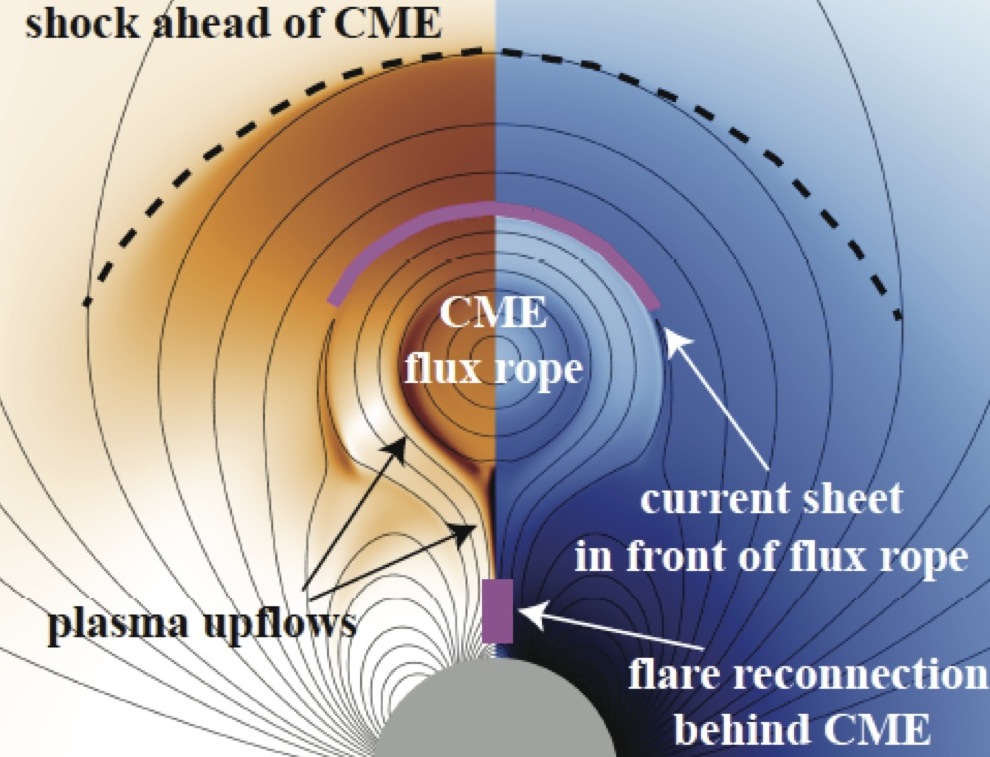
The 2D version of HiFi has been used for magnetic reconnection studies in electron-positron plasmas (Chacon et al. 2008), to identify and describe an electron MHD instability of reconnection separatrix layers (Lukin 2009), to self-consistently validate a new anisotropic electron equation of state against particle-in-cell simulations of collisionless magnetic reconnection (Ohia et al. 2012; Le et al. 2013; Ohia et al. 2016), and to model magnetic reconnection, including the onset of the plasmoid instability, in reacting weakly-ionized chromospheric plasmas (Leake et al. 2012; Leake et al. 2013; Murphy & Lukin 2015; Ni et al. 2018). 2D HiFi has also been used to model the Mega-Ampere Spherical Tokamak (Stanier et al. 2013; Browning et al. 2014; Browning et al. 2016; Kirk et al. 2017)  in a toroidal geometry, as well as to study solar coronal mass ejections (CMEs) in a highly stratified solar atmosphere (Lee et al. 2014) and the Rayleigh-Taylor instability in the Earth's ionosphere and the solar atmosphere (Leake et al. 2014).  2D HiFi simulations by Provornikova et al. 2016 investigate plasma compression and possible consequences for particle acceleration in magnetic reconnection sites in the lower solar atmosphere.

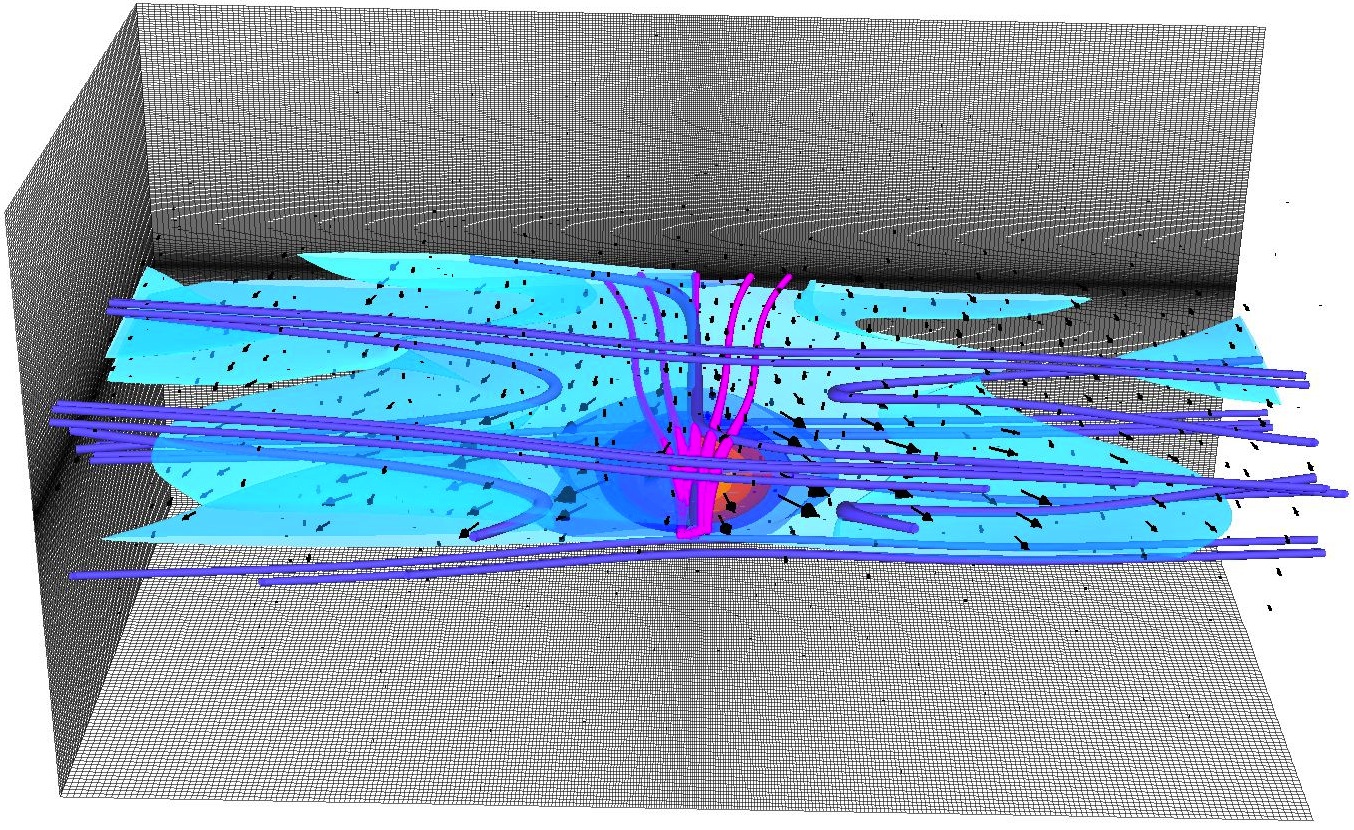
The 3D HiFi version has been used to perform non-linear MHD and Hall MHD simulations of several geometric configurations of the Swarthmore Spheromak Experiment (Cothran et al. 2010; Gray et al. 2010; Lukin & Linton 2011; Schaffner et al. 2014a; Schaffner et al. 2014b), and the ZaP flow Z-pinch experiment (Lowrie 2011; Shumlak et al. 2012; Knecht et al. 2014).  Akcay et al. 2016 conducted a 3D HiFi two-fluid study of oblique tearing modes in a force-free current sheet.

The HiFi framework has been used to address a variety of fluid-based computational plasma physics challenges in laboratory, space, and solar plasma environments. 

Development and applications of the HiFi framework have been the basis, or constituted a large fraction, of several Ph.D. dissertations:

Vyacheslav S. Lukin, Computational Study of the Internal Kink Mode Evolution and Associated Magnetic Reconnection Phenomena, PhD thesis, Princeton University, 2008;

Eric T. Meier, Modeling Plasmas with Strong Anisotropy, Neutral Fluid Effects, and Open Boundaries, PhD thesis, University of Washington, 2011;

Weston B. Lowrie, Development and Application of a Multi-Block High Order Finite Element Modeling Code as an Engineering Design Tool, PhD thesis, University of Washington, 2011;

Adam Stanier, Magnetic Reconnection and Particle Acceleration in Semi-Collisional Plasmas, PhD thesis, University of Manchester, 2013.

Obioma Ohia, Two-fluid Simulations of Magnetic Reconnection with a Kinetic Closure for the Electron Pressure Anisotropy, PhD thesis, Massachusetts Institute of Technology, 2014.

The core version of the HiFi Framework relies on three freely available, widely used, and portable libraries:

• MPI
• PETSc
  
• Parallel HDF5